Studio di funzione. Studiare una funzione significa determinare gli elementi caratteristici che ci permettono di disegnarne il grafico, a partire dalla sua espressione analitica y=f (x) y = f (x).. Per studiare il segno della funzione impostiamo la relazione. f (x) ≥ 0 → x e^ (|x|)ln (3+x) ≥ 0. che, a conti fatti, è una disequazione prodotto che si risolve studiando il segno di ciascun fattore e costruendo in seguito la tabella dei segni. • x ≥ 0 → x ≥ 0 ; • e^ (|x|) ≥ 0 → ∀ x∈R ; • ln (3+x) ≥ 0 → 3+x ≥ 1 → x ≥ −2.

Continuità di una funzione Andrea il Matematico

STUDIO DI FUNZIONE FACILE (funzione fratta) Dominio, intersezioni, studio del segno, limiti

Come trovare il periodo di una funzione goniometrica YouTube
Studio Del Segno Di Una Funzione Esercizi cleenrietta

Lezione di Analisi Definizione di continuità di una funzione in un punto YouTube

Lo studio del segno di una funzione YouTube

ESERCIZI SVOLTI GRAFICO COMPLETO DI UNA FUNZIONE Schemi di Matematica

Studio di Funzione YouTube

Studio del segno di una funzione YouTube

Come studiare il segno di una funzione YouTube

Studio del segno di una funzione razionale fratta Matematica delle scuole superiori, Analisi

Studio del segno di una funzione razionale fratta YouTube

PPT IL DOMINIO DI UNA FUNZIONE PowerPoint Presentation, free download ID5188557

Zeri di una Funzione YouTube
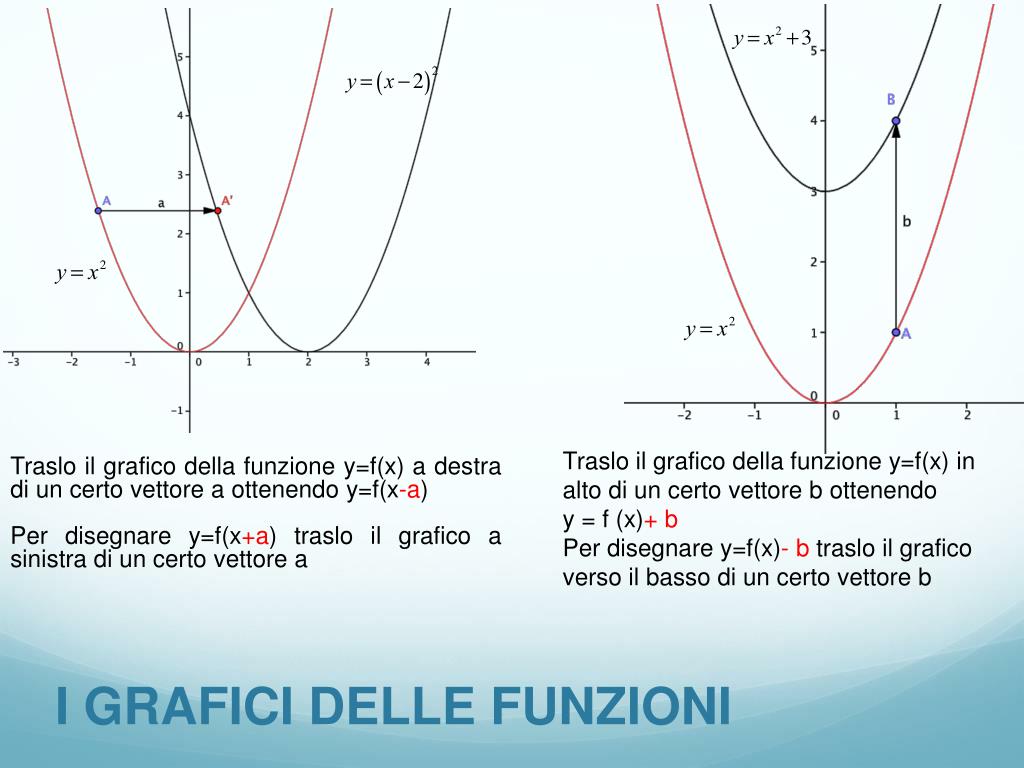
PPT LE FUNZIONI REALI DI VARIABILE REALE PowerPoint Presentation, free download ID746987

Matematica studio delle funzioni caso 4 (fino al segno della funzione) YouTube

Studio del segno Matematica Dolce
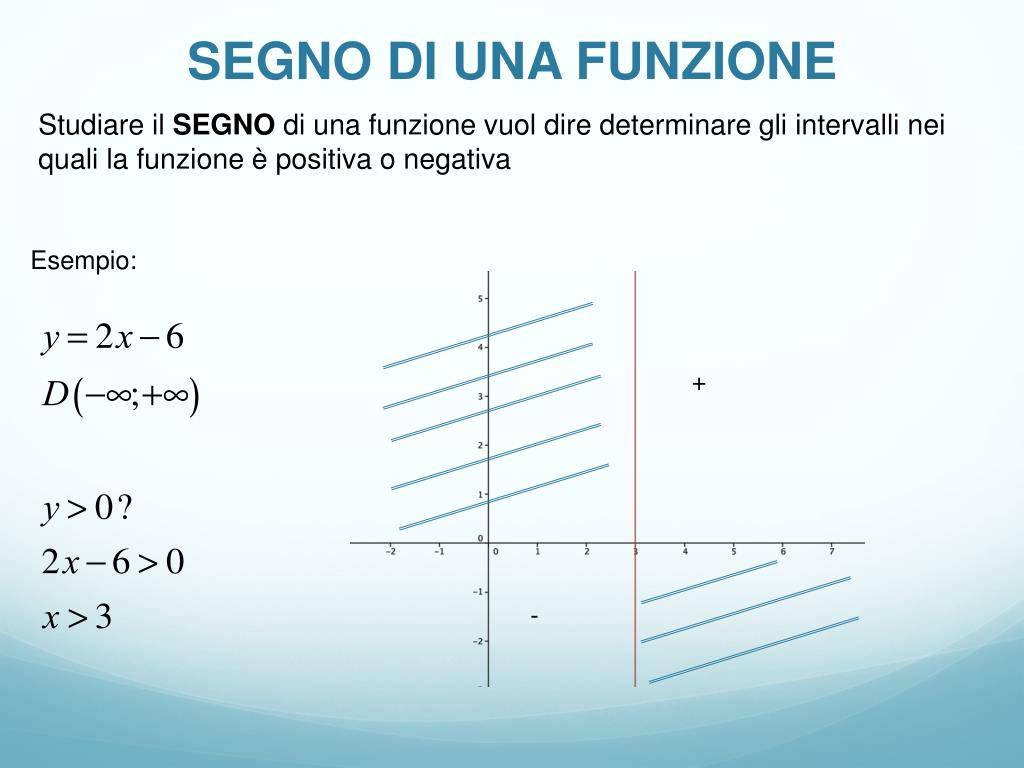
PPT LE FUNZIONI REALI DI VARIABILE REALE PowerPoint Presentation, free download ID746987

Studio di funzione razionale fratta dominio, segno, limiti YouTube

Funzioni definizione, come ricavare dominio, codominio da un grafico, funzione definita a
Passo 1: Calcoliamo la derivata prima della funzione: f’ (x) = 2x – 3. Passo 2: Studiamo il segno della derivata prima: Se f’ (x) > 0, la funzione è crescente. Se f’ (x) < 0, la funzione è decrescente. Se f' (x) = 0, la funzione presenta un punto di massimo o minimo.. Studio del segno di una funzione ed esempi svolti. Matematica per la scuola secondaria. Per visualizzare tutti i corsi realizzati da Opera Matematica potete accedere al seguente link: https.